Noval Gandhi S (201731236): April 2019

Teorema Substitusi

Pada teorema ini berlaku bahwa :

Suatu komponen atau elemen pasif yang dilalui oleh sebuah arus yang mengalir (sebesar i) maka pada komponen pasif tersebut dapat digantikan dengan sumber tegangan Vs yang mempunyai nilai yang sama saat arus tersebut melalui komponen pasif tersebut.

Jika pada komponen pasifnya adalah sebuah resistor sebesar R, maka sumber tegangan penggantinya bernilai Vs = i.R dengan tahanan dalam dari sumber tegangan tersebut Sama dengan nol.

Rangkaian berikut dapat dianalisa dengan teori substitusi untuk menentukan arus yang mengalir pada resistor 2Ω.

Harus diingat bahwa elemen pasif yang dilalui oleh sebuah arus yang mengalir (sebesar i) maka pada elemen pasif tersebut dapat digantikan dengan sumber tegangan Vs yang mempunyai nilai yang sama saat arus tersebut melaluinya. Kemudian untuk mendapatkan hasil akhirnya analisa dapat dilakukan dengan analisis mesh atau arus loop.

Respon Alami dan Respon Steady State

Ada beberapa istilah yang perlu dipahami :

1. Respon alami adalah respon yang hanya tergantung pada energy dalam yang disimpan elemen (Kapasitor dan induktor) dan bukan oleh sumber luar.

2. Respon steady state adalah respon yang muncul setelah rentang waktu yang lama.

3. Respon paksa adalah respon yang muncul karena reaksi satu atau lebih sumber bebasnya.

4. Respon transient atau respon peralihan adalah respon sementara yang muncul dalam waktu terbatas.

Konsep Fasa / Fase

Terdapat satu karakteristik utama dari pasokan listrik arus bolak-balik atau AC yang memerlukan penjelasan, yaitu: “fase”. Pada dasarnya pasokan listrik AC dibagi kedalam sirkuit satu fase dan tiga fase. Sirkuit AC satu fase memiliki dua buah kawat yang dihubungkan ke sumber listrik. Tidak seperti sirkuit DC yang arah arus listrik nya tidak berubah, maka dalam sirkuit AC arah arus berubah berkali-kali tiap detiknya tergantung pada frekuensi pasokan. Listrik 220 volt (V) yang dipasok ke rumah kita merupakan listrik AC satu fase dan memiliki dua buah kawat: ‘ aktif’ dan ‘ netral’ .

Sistim 3 fase memiliki 3 bentuk gelombang (biasanya membawa daya) yaitu 2/3 p radian (120 derajat, 1/3 siklus) untuk waktu tertentu.

Gambar 1. Sistem 3 fase

Gambar 1 menunjukan sistim satu siklus tiga fase, dari 0 hingga 360 derajat (2 p radians), sepanjang aksis waktu. Garis yang diplotkan menunjukan keragaman tegangan sesaat (atau arus) dalam waktu. Siklus ini akan berulang 50 atau 60 kali per detiknya, tergantung pada frekuensi sistem dayanya. Warna garis menyatakan kode pewarnaan Amerika untuk sistem tiga fase: hitam =VL1, merah=VL2 dan biru=VL3.

Sistem pasokan tiga fase selanjutnya dinyatakan oleh hubungan bintang dan delta seperti ditunjukkan dalam Gambar 2 dan 3.

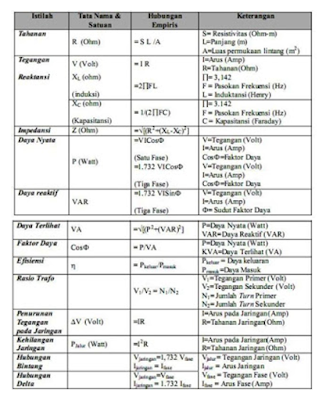
FORMULA LISTRIK

Tabel dibawah memuat daftar formula/ rumus paling penting untuk sistim listrik.

keterangan: klik gambar-gambar diatas untuk melihat lebih jelas, karena alasan kapasitas agar tidak membebani blog ini, maka ukuran gambar ditampilkan kecil.

ANALISIS RANGKAIAN AC

1. Hukum Ohm

Jika sebuah impedansi dilewati oleh sebuah arus maka pada kedua ujung impedansi

tersebut akan muncul beda potensial, atau Hukum Ohm menyatakan bahwa tegangan

melintasi berbagai jenis bahan pengantar adalah berbanding lurus dengan arus yang

mengalir melalui bahan tersebut.

Secara matematis :

V = I.Z

2. Hukum Kirchoff I / Kirchoff’s Current Law (KCL)

Jumlah arus yang memasuki suatu percabangan atau node atau simpul samadengan arus

yang meninggalkan percabangan atau node atau simpul, dengan kata lain jumlah aljabar

semua arus yang memasuki sebuah percabangan atau node atau simpul samadengan nol.

Secara matematis :

Σ Arus pada satu titik percabangan = 0

Σ Arus yang masuk percabangan = Σ Arus yang keluar percabangan

3. Hukum Kirchoff II / Kirchoff’s Voltage Law (KVL)

Jumlah tegangan pada suatu lintasan tertutup samadengan nol, atau penjumlahan

tegangan pada masing-masing komponen penyusunnya yang membentuk satu lintasan

tertutup akan bernilai samadengan nol.

Secara matematis :

ΣV = 0

DAYA PADA RLC

Rangkaian R L C - Rangkaian RLC adalah rangkaian elektronika yang didalamnya terdapat tiga buah komponen, yakni resistor, induktor, dan kapasitor. Rangkaian tersebut bisa dihubungkan dalam bentuk seri maupun paralel sesuai kebutuhan dari si pembuat rangkaian itu sendiri. Karakteristik Resistor, Induktor dan Kapasitor

Rangkaian RLC dapat membentuk sebuah sistem persamaan diferensial orde kedua atau bisa juga dua persamaan diferensial orde pertama, dimana persamaan diferensial tersebut diselesaikan secara simultan. Berikut adalah rumus frekwensi resonansi dari rangkaian RLC yang harus anda ketahui.

Dalam rangkaian RLC, kita mengenal dua jenis bagiannya yakni rangkaian RLC seri dan rangkaian RLC paralel. Perbedaan dari kedua rangkaian tersebut tentunya terletak pada penyusunan komponen resistor, induktor, dan kapasitornya, dimana yang satu dipasang secara seri, dan yang satunya lagi dipasang secara paralel.

Perbedaan model pemasangan tersebut bukan tanpa maksud. Terdapat beberapa perbedaan hasil yang ditampilkan oleh kedua rangkaian tersebut. Berikut ini adalah penjabaran lebih lanjut mengenai rangkaian RLC seri dan rangkaian RLC paralel secara lebih lengkap.

· Rangkaian RLC Seri

Rangkaian seri RLC adalah rangkaian elektronika yang tersusun atas resistor, induktor, dan kapasitor yang dihubungkan secara seri, dengan sumber tegangan bolak-balik atau tegangan AC. Pada rangkaian RLC seri, hambatan arus tegangan sefase, induktor tegangan mendahului arus, serta kapasitor tagangan didahului arus.

· Rangkaian RLC Paralel

Rangkaian seri RLC adalah rangkaian elektronika yang tersusun atas resistor, induktor, dan kapasitor yang dihubungkan secara paralel, dengan sumber tegangan bolak-balik atau tegangan AC. Pada rangkaian RLC paralel, terjadi pembagian arus listrik dari sumber menjadi tiga, yakni mengarah ke resistor, induktor, dan kapasitor.

Rangkaian R-L-C paralel, sifat dari rangkaian paralel adalah terjadi percabangan arus dari sumber (i) menjadi tiga, yaitu arus yang menuju arus yang menuju resistor (iR), induktor (iL) dan kapasitor (iC). Sedangkan tegangan jatuh pada resistor (vR), pada induktor (vL) dan pada kapasitor (vC) sama besar dengan sumber tegangan (v). Gambar rangkaian R-L-C parallel dibawah memperlihatkan hubungan arus secara vektoris pada rangkaian R-L-C paralel.

Suatu rangkaian arus bolak-balik yang terdiri dari resistor (R), reaktansi induktif (XL) dan reaktansi kapasitif (XC), dimana ketiganya dihubungkan secara paralel. Fasor tegangan (v) sebagai sumber tegangan total diletakan pada ωt = 0. Arus efektif (iR) berada sefasa dengan tegangan (v). Arus yang melalui reaktansi induktif (iL) tertinggal sejauh 900 terhadap tegangan (v) dan arus yang melalui reaktansi kapasitif (iC) mendahului sejauh 900 terhadap tegangan (v). Arus reaktif induktif (iL) dan arus reaktif kapasitif (iC) bekerja dengan arah berlawanan, dimana selisih dari kedua arus reaktif tersebut menentukan sifat induktif atau kapasitif suatu rangkaian. Arus gabungan (i) adalah jumlah geometris antara arus efektif (iR) dan selisih arus reaktif (iS) yang membentuk garis diagonal empat persegi panjang yang dibentuk antara arus efektif (iR) dan selisih arus reaktif (iS). Posisi arus (i) terhadap tegangan (v) ditentukan oleh selisih kedua arus reaktif (iS).

Bila arus yang melalui reaktansi induktif (iL) lebih besar daripada arus yang melalui reaktansi kapasitif (iC), maka arus total (i) tertinggal sejauh 900 terhadap tegangan (v), maka rangkaian paralel ini cenderung bersifat induktif. Sebaliknya bilamana arus yang melalui reaktansi induktif (iL) lebih kecil daripada arus yang melalui reaktansi kapasitif (iC), maka arus total (i) mendahului sejauh 900 terhadap tegangan (v), maka rangkaian paralel ini cenderung bersifat kapasitif.

Untuk menghitung hubungan seri antara R, XL dan XC pada setiap diagram fasor kita ambil segitiga yang dibangun oleh arus total (i), arus.selisih (iS) dan arus efektif (iR). Dari sini dapat dibangun segitiga daya hantar, yang terdiri dari daya hantar resistor (G), daya hantar reaktif (B) dan daya hantar impedansi (Y).

Sehingga hubungan arus (i) terhadap arus cabang (iR), (iL) dan (iC) dapat ditentukan dengan menggunakan persamaan kuadrat berikut;

Oleh karena arus reaktif (iS) adalah selisih dari arus reaktif (iL) dan arus reaktif (iC), maka daya hantar reaktif (B) adalah selisih dari daya hantar reaktif (BL) daya hantar reaktif (BC).

Untuk arus pada hubungan paralel berlaku persamaan

Arus efektif iR = v . G

Arus reaktif induktif iL = v . BL

Arus reaktif kapasitif iC = v. BC
Sudut fasa (ϕ) dapat dihitung dari persamaan

RANGKAIAN KOPLING MAGNETIK

Kutub 4

Salah satu aplikasi penting dari konsep network function adalah pada jaringan dimana sinyal input dan output diukur pada pasangan terminal yang berbeda.

Bentuk umum :

Jaringan 2 port dengan 4 terminal

• Adapun teori rangkaian (K-4) ini banyak dipergunakan pada jaringan yang dipergunakan dalam sistem komunikasi, sistem daya, sistem kontrol dan rangkaian elektronik (model transistor).

• Pada rangkaian (K-4) ini banyak memerlukan hubungan antara V₁, V₂, I_1,dan I₂ yang saling independent, dimana berbagai macam hubungan antara tegangan dan arus disebut sebagai parameter.

Jaringan 2 port dengan 3 terminal

1. Parameter Z

2. Parameter Y

3. Parameter hybrid

4. Paramater ABCD

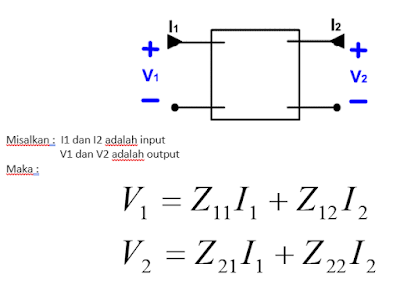
Parameter Z

Parameter Z (cont.)

Impedansi yang dihasilkan sebagai impedansi open circuit atau parameter open circuit atau parameter Z.

Z11 = impedansi port primer ketika port sekunder open circuit

Z22 = impedansi port sekunder ketika port primer open circuit

Z12 = Z21 = impedansi transfer dimana perbandingan tegangan disatu ortu dibandingkan arus di port lainnya.

Parameter Y

Misalkan : V1 dan V2 adalah input

I1 dan I2 adalah output

Maka :

Parameter Y (cont.)

· Kutub 4 juga dapat dinyatakan tanpa menggunakan impedansi atau admintasi, yakni hanya menggunakan variabel tegangan dan arus yaitu parameter transmisi (ABCD)

· V1= A V2. B V2

· I1= C V2. D V2

· Parameter ini penting untuk teknik transmisi, sebab disisi primer (pengirim) terdiri dari variabel V1dan I1, sedangkan (penerima) terdiri dari variabel V2dan I2(negatif I2karena arus masuk ke beban penerima)

Respon Frekuensi Dan Resonansi

Respon frekuensi merupakan hubungan atau relasi frekuensi tak bebas pada kedua

besaran magnitude dan phasa diantara input sinusoidal steady state dan output

sinusoidal steady state.

Rangkaian RL

Rangkaian RC

Rangkaian RLC

Resonansi

Suatu rangkaian dikatakan beresonansi ketika tegangan terpasang V dan arus yang dihasilkan I dalam kondisi satu phasa.

Misalkan :

Terlihat bahwa ketika V dan I satu phasa, impedansi yang dihasilkan seluruhnya komponen riil atau impedansi kompleks hanya terdiri dari komponen resistor murni (R). Dengan kata lain konsep resonansi adalah menghilangkan komponen imaginer /reaktansi saling meniadakan.

Frekuensi Kompleks

CONTOH SOAL

1. rangkaian listrik kompleks
dik : +- 100v
+- -50v
arus 5A
hambatan 5ohm
dit : arus pada tegangan -50v
jwb : arus pada hambatan 5ohm ( -50 = -50/5 =-10A
sumber arus 5A mempunyai tegangan = -(-50v)+100v= 150v
sumber arus hambatan 5ohm = 150/5= 30A
besar arus pada tegangan -50 = (30+5)-5 = 35-5 =30A

2. konsep dasar
A)

Kuat arus listrik (I) pada rangkaian

B) Sebuah sumber tegangan bolak balik mempunyai frekuensi 50 Hz dan tegangan maksimum 100V dihubungkan dengan komponen RLC dengan R = 9 ohm, L = 0.04 H, dan 100 µF.tentukan Tegangan maksimum dalam dalam setiap komponen!

Sebelum menghitung tegangan maksimum, hitung terlebih dahulu arus maksimum.

Tegangan maksimum pada masing-masing komponen RLC

3). Hukum ohm
Kawat penghantar kedua ujungnya memiliki beda potensial 75 volt, menyebabkan arus listrik mengalir pada kawat itu 5 A. Berapakah hambatan kawat itu?
dik : v=75v
i = 5A
dit: R
jwb: R=V/I
= 75/5

= 15ohm

4). hukum kirchoff 1

Perhatikan gambar di atas, pada titik P dari sebuah rangkaian listrik ada 4 cabang, 2 cabang masuk dan 2 cabang keluar. Jika diketahui besarnya I1 = 16 A, I2 = 4 A, dan I3 = 10 A, tentukan berapa besar nilai dari I4?

Jawab

Diketahui

I1 = 16A
I2 = 4 A
I3 = 10 A

Ditanya I4 = …?
Hukum Kirchoff I

ΣImasuk = ΣIkeluar

I1 + I2 = I3 + I4
16 + 4 = 10 + I4
20 = 7 + I4
I4 = 20-7 = 13A

5). hukum kirchoff 2
Hitunglah berapa kekuatan arus yang mengalir pada sebuah rangkaian arus listrik jika R1 = 11 Ώ, R2 = 12 Ώ, dan R13 = 6 Ώ.

(R1 – E1) + ɩ (R2) + ɩ (R3 + E2) = 0

(R1 +R2 + R3 + (E1– E2) = 0

(11Ώ + 12 Ώ + 13 Ώ) + 3V – 9V = 0

36 ɩ – 6V = 0

30 = 6V

6). elemen aktif

suatu rangkaian arah arus sebesar 22A,33A,dan 44A. hambatan 9 ohm,3 ohm,6 ohm. dengan ada V sebagai + dan - nya. berapa v nya?

nilai V
arus resistor 3ohm
44A-22A=22A
v= 22x3=66v

7). elemen pasif

Resistor

1. Setting DC Generator atau Power Supply untuk menghasilkan sebuah Output Tegangan 10V, kemudian atur nilai Potensiometer ke 2 kiloOhm. Berapakah nilai Arus Listrik (I)?
V = 10 V
R = 2 KiloOhm = 2000 Ω
Jawab :
I = V / R
I = 10 / 2000
I = 0.02 Ampere atau 20 miliAmpere

koneksitor